how to find standard deviation in statistics

Standard Departure

Standard departure is the positive square root of the variance. Standard deviation is one of the basic methods of statistical analysis. Standard departure is commonly abbreviated as SD and denoted by 'σ' and it tells almost the value that how much it has deviated from the hateful value. If we go a low standard departure then it means that the values tend to be close to the mean whereas a high standard deviation tells us that the values are far from the mean value. Permit us learn to calculate the standard divergence of grouped and ungrouped data and the standard deviation of a random variable.

1.	What is Standard Deviation?
2.	Standard Deviation Formula
3.	Standard Deviation of Random Variables
iv.	Standard Deviation of Probability Distribution
5.	FAQs on Standard Deviation

What is Standard Deviation?

Standard deviation is the degree of dispersion or the scatter of the data points relative to its mean, in descriptive statistics. It tells how the values are spread beyond the information sample and it is the measure of the variation of the information points from the mean. The standard divergence of a sample, statistical population, random variable, data set, or probability distribution is the square root of its variance.

When we accept n number of observations and the observations are \(x_1, x_2, .....x_n\), and so the mean deviation of the value from the mean is determined equally \(\sum_{i=1}^{n}\left(x_{i}-\bar{10}\right)^{2}\). Nevertheless, the sum of squares of deviations from the mean doesn't seem to be a proper measure of dispersion. If the average of the squared differences from the mean is small, information technology indicates that the observations \(x_i\) are close to the mean \(\bar 10\). This is a lower caste of dispersion. If this sum is large, it indicates that there is a higher degree of dispersion of the observations from the mean \(\bar x\). Thus we conclude that \(\sum_{i=1}^{n}\left(x_{i}-\bar{10}\right)^{2}\) is a reasonable indicator of the degree of dispersion or scatter.

Nosotros take \(\dfrac{i}{northward}\sum_{i=1}^{n}\left(x_{i}-\bar{x}\correct)^{two}\) equally a proper measure of dispersion and this is called the variance(σ²). The square root of the variance is the standard deviation.

Steps to Calculate Standard Deviation

• Find the mean, which is the arithmetic mean of the observations.
• Discover the squared differences from the mean. (The data value - hateful)ⁱⁱ
• Detect the average of the squared differences. (Variance = The sum of squared differences ÷ the number of observations)
• Discover the square root of variance. (Standard deviation = √Variance)

Standard Deviation Formula

The spread of statistical information is measured by the standard deviation. The degree of dispersion is computed by the method of estimating the deviation of information points. You tin can read virtually dispersion in summary statistics. As discussed, the variance of the data set is the average square distance between the mean value and each data value. And standard difference defines the spread of information values effectually the mean. Here are two standard departure formulas that are used to find the standard deviation of sample data and the standard difference of the given population.

Formula for Computing Standard Deviation

The population standard departure formula is given as:

• \(\sigma=\sqrt{\frac{1}{N} \sum_{i=1}^{Due north}\left(X_{i}-\mu\right)^{2}}\)

Here,

• σ = Population standard deviation
• μ = Assumed mean

Similarly, the sample standard deviation formula is:

• \(s=\sqrt{\frac{i}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}\)

Here,

s = Sample standard departure

\(\bar 10\) = Arithmetic mean of the observations

Standard Deviation of Ungrouped Data

The calculations for standard deviation differ for different data. Distribution measures the deviation of information from its hateful or average position. There are 2 methods to find the standard difference.

• actual hateful method
• causeless mean method

Standard Deviation by The Actual Hateful Method

σ = √(∑\(ten-\bar ten)\)² /northward)

Consider the information observations 3, 2, 5, half-dozen. Hither the mean of these data points is 16/iv = four.

The squared differences from hateful = (iv-3)ⁱⁱ+(2-4)² +(v-4)² +(half dozen-4)²= 10

Variance = Squared differences from mean/ number of information points =ten/4 =2.5

Standard deviation = √2.5 = i.58

Standard deviation by Assumed Hateful Method

When the x values are big, an arbitrary value (A) is chosen as the mean. The deviation from this assumed mean is calculated as d = ten - A.

σ = √[(∑(d)^two /n) - (∑d/north)²]

Standard Deviation of Grouped Data

When the information points are grouped, we first construct a frequency distribution.

Standard Deviation of Grouped Discrete Frequency Distribution

For n number of observtions, \(x_1, x_2, .....x_n\), and the frequency, \(f_1, f_2, f_3, ...f_n\) the standard divergence is:

\(\sigma=\sqrt{\frac{1}{North} \sum_{i=1}^{Northward}f_i \left(X_{i}-\bar ten\right)^{2}}\). Hither N = \(\sum_{i=1}^{N}f_i\)

Example: Let'south calculate the standard departure for the data given below:

\(x_i\)	6	ten	12	xiv	24
\(f_i\)	two	3	4	5	4

Calculate mean(\(\bar x\)): (6+8 +10+12+ 14)/5 = 10

\(x_i\)	\(f_i\)	\(f_ix_i\)	\(x_i -\bar x\)	\((x_i -\bar x\))2	\(f_i (x_i -\bar ten)\)ii
6	ii	12	-4	16	32
8	three	24	-ii	4	12
10	iv	40	0	0	0
12	5	lx	2	4	20
14	4	56	four	16	64
	18	192			128

N = 18, ∑\(f_i x_i\) = 192, ∑\(f_i (x_i -\bar x\))² = 128

Calculate variance: σ² = 1/N \(\sum_{i=1}^{N}f_i \left(X_{i}-\bar ten\correct)^{2}\)

= 1/xviii × 128 = 7.1

Calculate SD: σ = √Variance = √ seven.1 = two.66

Standard Deviation of Grouped Continuous Frequency Distribution

If the frequency distribution is continuous, each course is replaced by its midpoint. Then the Standard difference is calculated by the aforementioned technique equally in detached frequency distribution. Consider the following instance. \(x_i\) is calculated as the midpoint of each grade. Then the aforementioned standard deviation formula is practical.

Class	\(f_i\)	\(x_i\)
0-10	iii	5
x-20	4	15
20-thirty	6	25
thirty-40	four	35
forty-fifty	viii	twoscore

Standard Deviation of Random Variables

The measure of spread for the probability distribution of a random variable determines the degree to which the values differ from the expected value. This is a function that assigns a numerical value to each outcome in a sample space. This is denoted by Ten, Y, or Z, as information technology is a function. If X is a random variable, the standard deviation is determined past taking the square root of the sum of the product of the squared difference between the random variable, 10, and the expected value (𝜇) and the probability associated value of the random variable.

The standard deviation of the probability distribution of X, 𝜎 = \(\sqrt{(x - 𝜇)^2 P(10=x)}\)

This is besides equivalent to 𝜎 = \(\sqrt{E(10)^ii-[Eastward(X)]^2}\)

Standard Deviation of Probability Distribution

The experimental probability consists of many trials. When the difference betwixt the theoretical probability of an result and its relative frequency get closer to each other, nosotros tend to know the average outcome. This mean is known every bit the expected value of the experiment denoted by 𝜇.

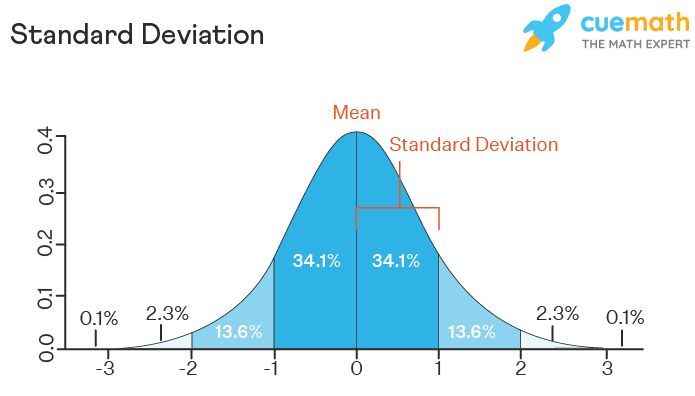
• In a normal distribution, the mean is zero and the standard divergence is 1.
• In a binomial experiment, the number of successes is a random variable. If a random variable has a binomial distribution, its standard divergence is given by: 𝜎= √npq, where mean: 𝜇 = np, north = number of trials, p = probability of success and 1-p =q is the probability of failure.
• In a Poisson distribution, the standard difference is given by 𝜎= √λt, where λ is the average number of successes in an interval of fourth dimension t.

Standard Deviation Tips:

• For n as the sample or the population size, the square root of the average of the squared differences of data observations from the mean is called the standard divergence.
• Standard deviation is the positive foursquare root of variance.
• Standard deviation is the indicator that shows the dispersion of the information points about the hateful.

☛ Besides Check:

• Sample Standard Deviation Formula
• Variance and Standard Deviation
• Probability and Statistics

Standard Departure Examples

1. Example 1: At that place are 39 plants in the garden. A few plants were selected randomly and their heights in cm were recorded every bit follows: 51, 38, 79, 46, 57. Calculate the standard deviation of their heights.

   Solution:

   N = five

   Mean (\(\bar{x}\))= (51+38+79+46+57)/5 = 54.2

   Standard Deviation = \( \sqrt{\dfrac{\Sigma (x_i-\bar{x})^2}{N-1}} \)

   = \( \sqrt{\frac{(51-54.2)^2 +(38-54.2)^2 +(79-54.2)^two +(46-54.2)^2 +(57-54.2)^2}{iv}} \)

   = 15.5

   Answer: Standard Difference for this data is 15.5

2. Case 2: In a class of 50, four students were selected at random and their full marks in the final assessments are recorded, which are: 812, 836, 982, 769. Find the standard deviation of their marks.

   Solution:

   N = four

   Sample Hateful (X̄) = (812+836+982+769)/iv = 849.75

   Variance = \( \dfrac{\sum^{Northward}_{i=1} (X_i - \bar{X})^2}{N-1} \)

   =\( \dfrac{\sum^{4}_{i=one} (X_i - 849.75)^2}{3} \)

   = [(812 - 849.75)ⁱⁱ + (836 - 849.75)² + (982 - 849.75)² + (769 - 849.75)²] /3 = 92.4

   Using the standard divergence formula,

   Standard Deviation = √92.4 = two √23.1 = 9.vi

   Respond: Standard Deviation for this data is 9.vi

3. Example 3: Find the standard difference of X which has the probability distribution as shown in the table beneath.

   X	P(10)
   2	0.2
   iii	0.3
   4	0.five

   Solution:

   To find the expected value of Ten, find the product X. P(10) and sum these terms.

   X	P(Ten)	10. P(X)
   4	0.2	0.viii
   5	0.iii	1.5
   6	0.four	two.4

   Eastward(Ten) = 0.eight+1.v+2.4

   =4.7

   Ten	P(X)	(Ten - East(Ten)2)	(X - E(X)2). P(Ten)
   four	0.2	4.9	0.98
   5	0.iii	0.9	0.27
   half-dozen	0.5	1.69	0.845

   Standard Departure = √(0.98+0.27+0.845)

   = √2.095 ≈1.45

   Answer:The standard deviation of the probability distribution is 1.45

go to slidego to slidego to slide

Have questions on basic mathematical concepts?

Become a problem-solving champ using logic, not rules. Learn the why behind math with our certified experts

Book a Complimentary Trial Class

Practice Questions on Standard Divergence

go to slidego to slide

FAQs on Standard Departure

What is Standard Deviation?

The standard deviation is the measure out of dispersion or the spread of the data about the hateful value. It helps united states to compare the sets of data that have the aforementioned mean just a different range. The sample standard divergence formula is: \(s=\sqrt{\frac{one}{northward-1} \sum_{i=one}^{north}\left(x_{i}-\bar{x}\right)^{two}}\), where \(\bar x\) is the sample mean and \(x_i\) gives the data observations and northward denotes the sample size.

How Exercise You Calculate Standard Difference?

For n observations in the sample, notice the mean of them. Discover the difference in mean for each information point and square the differences. Sum them up and find the foursquare root of the boilerplate of the squared differences. This is given as \(s=\sqrt{\frac{1}{n-one} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}\).

Give an Example of Standard Deviation

If nosotros become a low standard deviation and then information technology means that the values tend to be close to the mean whereas a high standard departure tells us that the values are far from the hateful value. Consider data points one, iii, 4, 5. The mean is 13/iv = iii.25. The average of mean differences = [(3.25-1)² + (3-3.25)^two+ (four-3.25)^two + (5-3.25)²]/iv = 2.06. The standard deviation = √2.06 = 1.43

What Is the Difference Betwixt Standard Departure Formula and Variance Formula?

Variance is the average squared deviations from the mean, while standard divergence is the foursquare root of this number. Both measures reflect variability in distribution, merely their units differ: Standard divergence is expressed in the same units as the original values (e.g., minutes or meters). Sample standard deviation formula = \(\sigma=\sqrt{\frac{1}{Due north-1} \sum_{i=ane}^{N}\left(X_{i}-\mu\correct)^{two}}\) and variance formula = σ^two = Σ (xi – x̅)²/(northward-i)

What Is Mean-Variance and Standard Difference in Statistics?

Variance is the sum of squares of differences between all numbers and ways...where μ is Mean, N is the total number of elements or frequency of distribution. Standard Deviation is the foursquare root of variance. It is a measure of the extent to which data varies from the mean. The standard Divergence formula is √variance, where variance = σ² = Σ (xi – x̅)ⁱⁱ/north-one

Which Is Better to Use Variance Formula or Standard Deviation Formula?

They each accept dissimilar purposes. The SD is usually more useful to draw the variability of the data while the variance is usually much more useful mathematically. For example, the sum of uncorrelated distributions (random variables) also has a variance that is the sum of the variances of those distributions.

Why Practice Nosotros Employ Standard Divergence Formula and Variance?

Standard departure looks at how spread out a group of numbers is from the mean, by looking at the square root of the variance. The variance measures the average caste to which each bespeak differs from the mean—the average of all information points.

Source: https://www.cuemath.com/data/standard-deviation/

Posted by: amadorhagerre1998.blogspot.com

Share this post